SDM-LKM Equivalence

7.4. SDM-LKM Equivalence#

7.4.1. Relation among DSM, LKM and EDM#

With regard to the relation to the stochastic models, there is a notable paper [FCD04] which suggests:

\[ SDM \sim LKM \supseteq EDM \]

Note

This equivalence, in our application, is under investigation.

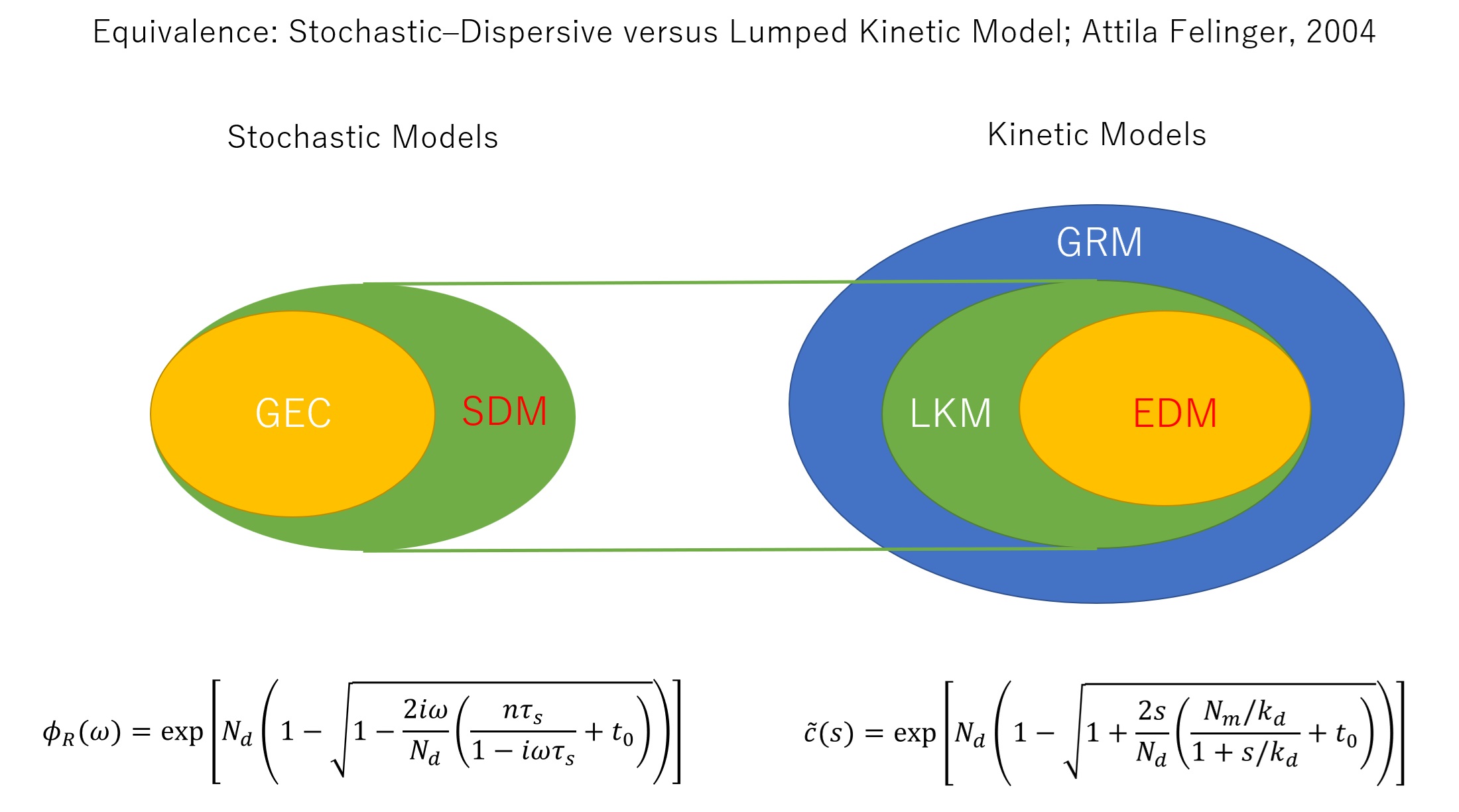
../../_images/sdm-lkm-equivalence.jpg

Fig. 7.2 SDM-LKM Equivalence#

7.4.2. Notational Correspondence in Relevant Papers#

Here are summarized notational correspondence among the relevant papers:

Table 7.3 Summary of Notational Correspondence between SDM and { LKM \(\supseteq\) EDM }#

Dondi-2002 SDM

Felinger-2004 LKM

Rehman-2021 EDM

Parameter Despription

\( N_0 \)

\( N_d = \frac{Lu}{2D} \)

\( \frac{Lu}{2D_z} \)

Number of Plates in Mobile Zone; \( N_0 = N_d = (\frac{t_0}{\sigma_0})^2 \)

\( n_i \)

\( N_m \)

Average Number of Stays in Stagnant Zone; \(N_m=F k_a t_0 = k' k_d t_0 \); \( k' = \frac{F k_a}{k_d} \)

\( \tau_i \)

\(\frac{1}{k_d} \)

Average Time of Stays in Stagnant Zone; \( \frac{1}{k_d} = \frac{k' t_0}{N_m} \)

\( K_{SEC} \)

\( e \) (porosity)

\( e \) (porosity)

\( \rho = \min(1, \frac{R_g}{R_p}) \) ; \( K_{SEC} = (1 - \rho)^m \) ; \( (K_{SEC})^{\frac{1}{m}} = 1 - \rho \) ; \( R_g \sim R_p(1 - porosity^{\frac{1}{m}}) \)

7.4.3. SymPy Examples to Understand the Papers#

To follow the papers, you can use SymPy. Here are some examples.

from sympy import symbols, Eq, Function, dsolve

f, g = symbols("f g", cls=Function)
x = symbols("x")
eqs = [Eq(f(x).diff(x), g(x)), Eq(g(x).diff(x), f(x))]
dsolve(eqs, [f(x), g(x)])

[Eq(f(x), -C1*exp(-x) + C2*exp(x)), Eq(g(x), C1*exp(-x) + C2*exp(x))]

dsolve(eqs, [f(x), g(x)], ics={f(0): 1, g(2): 3})

[Eq(f(x), (1 + 3*exp(2))*exp(x)/(1 + exp(4)) - (-exp(4) + 3*exp(2))*exp(-x)/(1 + exp(4))),
 Eq(g(x), (1 + 3*exp(2))*exp(x)/(1 + exp(4)) + (-exp(4) + 3*exp(2))*exp(-x)/(1 + exp(4)))]

eqn = Eq(f(x).diff(x), f(x))
dsolve(eqn, f(x), ics={f(x).diff(x).subs(x, 1): 2})
\[\displaystyle f{\left(x \right)} = \frac{2 e^{x}}{e}\]
from sympy import symbols, Function, dsolve
t = symbols('t')
y = Function('y')(t)
y
\[\displaystyle y{\left(t \right)}\]
yp = y.diff(t)
ypp = yp.diff(t)
eq = ypp + 2*yp + y
eq
\[\displaystyle y{\left(t \right)} + 2 \frac{d}{d t} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)}\]
dsolve(eq, y)
\[\displaystyle y{\left(t \right)} = \left(C_{1} + C_{2} t\right) e^{- t}\]
dsolve(eq, y, ics={y.subs(t, 0): 0})
\[\displaystyle y{\left(t \right)} = C_{2} t e^{- t}\]
Contents