Central Moment

5.1. Central Moment#

This section is a numerical introduction to the concept of central moment in the chromatographic context. Symbolic calculation will later be introduced using SymPy.

5.1.1. Simple Numerical Examples#

By “chromatographic context”, the following points are suggested.

  • We will consider the averaging of retention time (x axes in the following figures),

  • weighted by concentration (y axes).

Uniformly weighted Average#

import numpy as np
import matplotlib.pyplot as plt

N = 5
x = np.arange(N)
w = np.ones(N)     # uniform weights
plt.bar(x, w)
m = np.mean(x)
s = np.std(x)
plt.axvline(m, color='red')
for p in m-s, m+s:
    plt.axvline(p, color='yellow')
../../_images/64785597502ba869fc77cd1c3572e1f4468519908e7d3c65b4e4c92982d81b9f.png

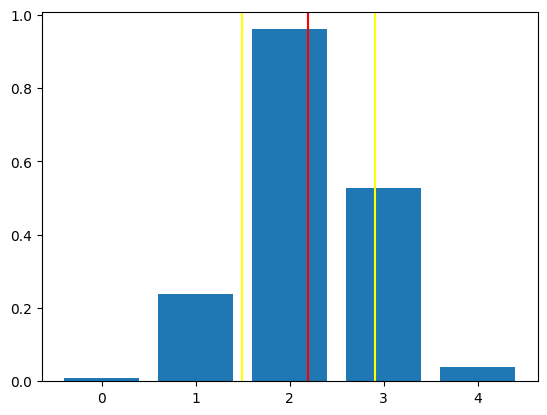
Averaging with Guassian Weights#

w = np.exp(-(x-2.2)**2)    # non-uniform (gaussian) weights

u = 0
v = 0
for i in range(N):
    u += w[i]*x[i]
    v += w[i]

m = u/v

z = 0
v = 0
for i in range(N):
    z += w[i]*(x[i] - m)**2
    v += w[i]
    
v, z, z/v, np.sqrt(z/v)

s = np.sqrt(z/v)
plt.bar(x, w)
plt.axvline(m, color='red')
for p in m-s, m+s:
    plt.axvline(p, color='yellow')
../../_images/191813d9bf812a9d503c905a9bfb2962e568165351edde8f8e406fb237b92379.png

5.1.2. Do it faster in NumPy#

0th Raw Moment#

M0 = np.sum(w)
M0

1.772080571028074

1st Raw Moment or Mean#

M1 = np.sum(w*x)/M0
M1

2.199132225263884

2nd Central Moment and Standard Deviation#

M2 = np.sum(w*(x - M1)**2)/M0
M2, np.sqrt(M2)

(0.49785237938665794, 0.7055865498906976)
Contents