Form and Structure Factors

6.3. Form and Structure Factors#

6.3.1. General Note#

Note

This section is planned.

References:

6.3.2. Definition for SEC-SAXS Solution Context#

For the discussion in the following chapters, the definitions of form factor and structure factor are presented here. According to [GJF21], these two factors are pedagogically distinguished as follows:

  • form factor — scattering by individual particles

  • structure factor — scattering by collections of particles

In simple terms, we can understand them pragmatically as:

  • \( I(q) \sim P(q) \) when interpaticle effects are ignored (i.e., \(S(q)=1\) in this case)

  • \( I(q) \sim P(q)S(q) \) when interpaticle effects are considered.

6.3.3. Form Factor#

For an individual particle, the form factor is defined as

\[ I(q) = \rho^2V^2P(q) \qquad \qquad (1) \]

where

  • \(I(q)\) : scattered intensity

  • \(\rho\) : electron density

  • \(V\) : particle volume

  • \(P(q)\) : form factor (normalized so that P(q) = 1 for small q).

For a sample, ignoring interparticle effects, it can be written as

\[ I(q) = c\rho^2V^2P(q) \qquad \qquad (2) \]

where

  • \(c\) : particle concentration.

6.3.4. Structure Factor#

When you consider the interparticle effects, they are expressed as

\[ I(q) = c\rho^2V^2P(q)S(q) \qquad \qquad (3) \]

where

  • \(S(q)\) : structure factor.

In other words, we can just think that the structure factor is a reprentaion of interparticle effects.

6.3.5. Form Factor Models#

Following [Ped97], we will give some known examples of form factor models.

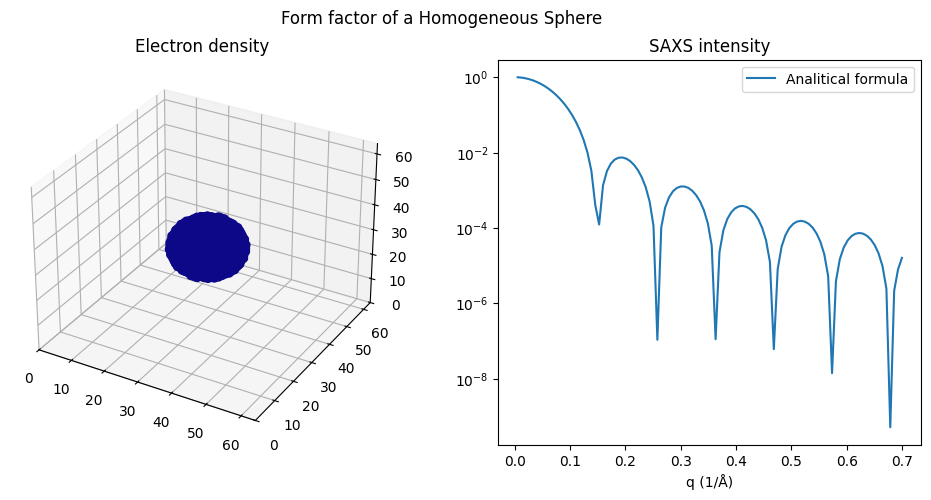
Homogeneous Sphere#

from molass import get_version
assert get_version() >= '0.5.0', "This tutorial requires molass version 0.5.0 or higher."
import numpy as np
import matplotlib.pyplot as plt
from molass.Shapes import Sphere
from molass.DensitySpace import VoxelSpace
from molass.SAXS.Models.Formfactors import homogeneous_sphere

q = np.linspace(0.005, 0.7, 100)
R = 30

I = homogeneous_sphere(q, R)

sphere = Sphere(radius=10)
space = VoxelSpace(64, sphere)

fig = plt.figure(figsize=(12, 5))
fig.suptitle('Form factor of a Homogeneous Sphere')
ax1 = fig.add_subplot(121, projection='3d')
ax1.set_title('Electron density')
space.plot_as_dots(ax1)

ax2 = fig.add_subplot(122)
ax2.set_title('SAXS intensity')
ax2.set_yscale('log')
ax2.plot(q, I, label='Analitical formula')
ax2.legend()
ax2.set_xlabel('q (1/Å)')

Text(0.5, 0, 'q (1/Å)')
../../_images/2724abafbba69e09fccd86a10ab352b6e91f7bebc1c9f158a3c8747bc824e57c.png

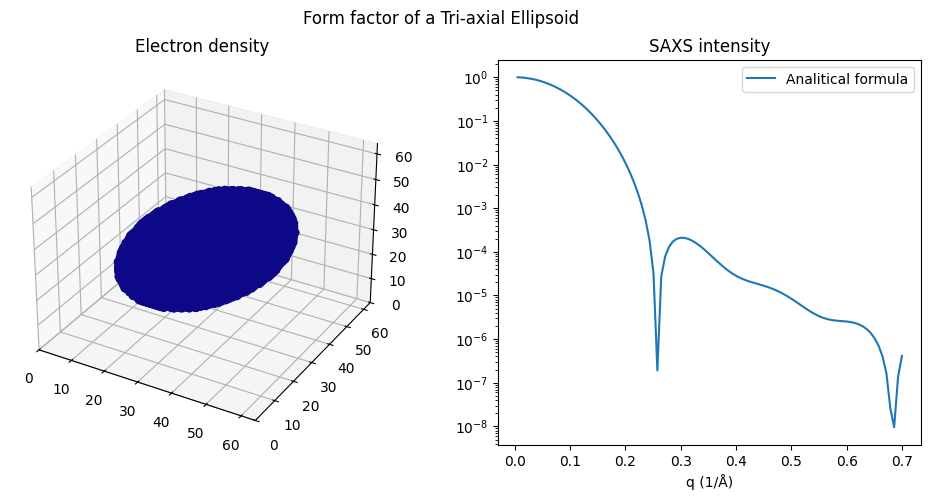
Tri-axial Ellipsoid#

from molass.Shapes import Ellipsoid
from molass.DensitySpace import VoxelSpace
from molass.SAXS.Models.Formfactors import tri_axial_ellipsoid
I = tri_axial_ellipsoid(q, 30, 20, 10)

ellipsoid = Ellipsoid(30, 20, 10)
space = VoxelSpace(64, ellipsoid)

fig = plt.figure(figsize=(12, 5))
fig.suptitle('Form factor of a Tri-axial Ellipsoid')
ax1 = fig.add_subplot(121, projection='3d')
ax1.set_title('Electron density')
space.plot_as_dots(ax1)

ax2 = fig.add_subplot(122)
ax2.set_title('SAXS intensity')
ax2.set_yscale('log')
ax2.plot(q, I, label='Analitical formula')
ax2.legend()
ax2.set_xlabel('q (1/Å)')

Text(0.5, 0, 'q (1/Å)')
../../_images/de8083c7d460020b333cb2392c1f5928c60b1735ba0d8d427ba85e2529b628ed.png

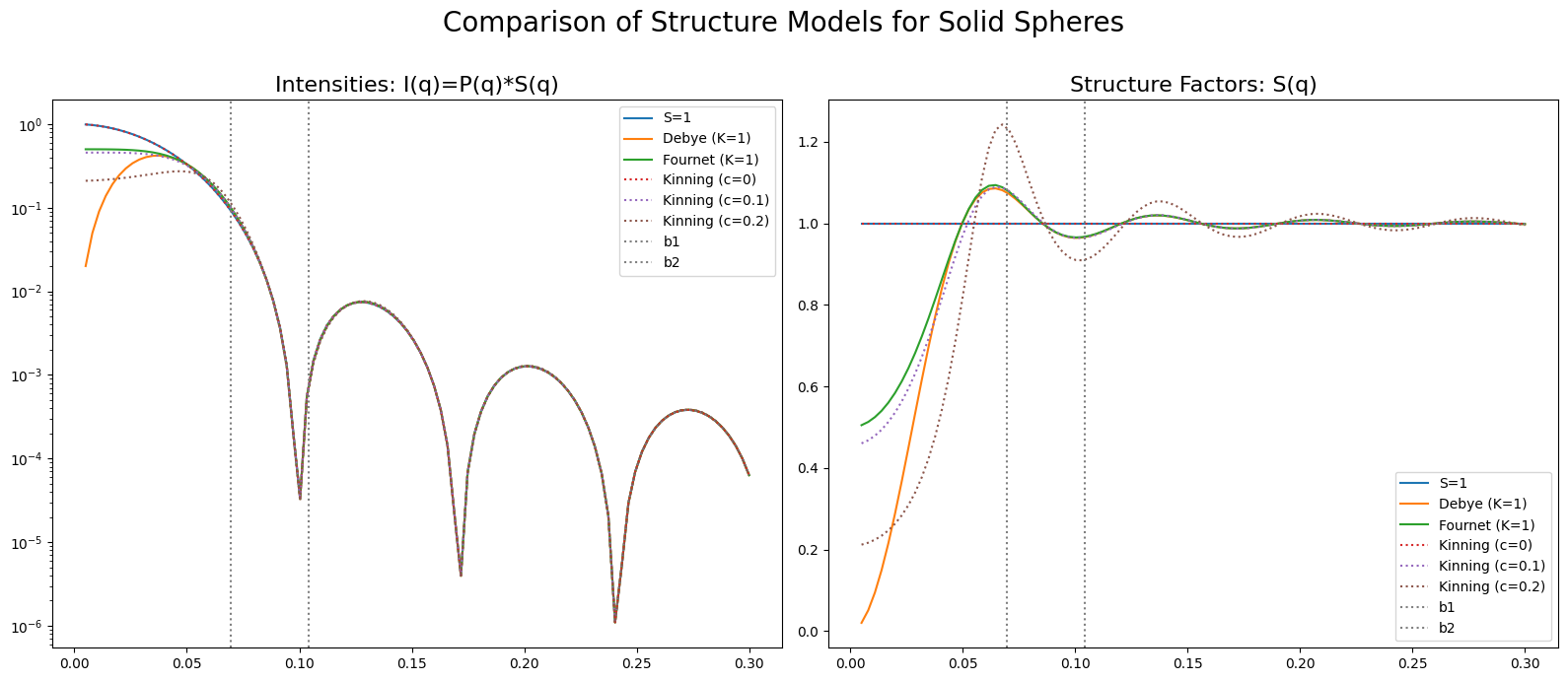
6.3.6. Structure Factor Models#

Following [KT84], we will give some known examples of structure factor models.

from molass import get_version
assert get_version() >= '0.5.0', "This tutorial requires molass version 0.5.0 or higher."
from molass.SAXS.Theory.DjKinning1984 import demo1
demo1()
../../_images/a66d3fc55293290be7ada71b37e557dc27861a65fd4c6890a45a448b019d23ed.png
Contents