Rank Estimation

6. Rank Estimation#

If interparticle interaction effects can be ignored, the rank of the data set (as a matrix) can be considered equal to the number of components. For example under such assumption, if the number of components is two, the rank is also two. In this sense, the rank of UV data is equal to the number of components because interparticle effects are known to appear only for X-ray data (in this UV vs. X-ray contrast).

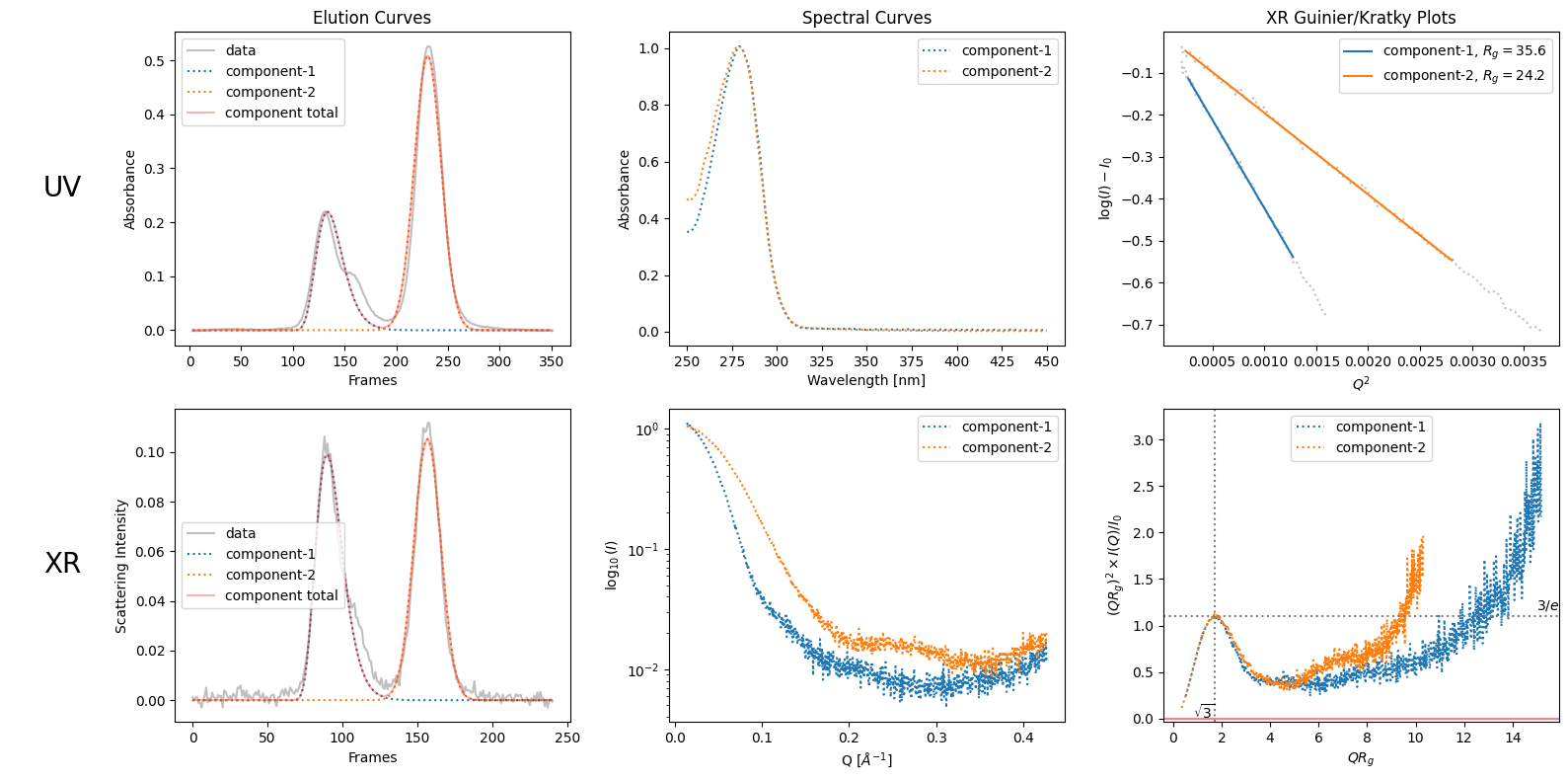
To put it practically, what we usually have to do is such that we will first idetify the component peaks by decomposition and then decide the rank of each component peak to be either 1 ro 2. For example, in the case of “SAMPLE1” data, the ranks of component peaks are suumarized in the table below in the order of elution.

component peak

rank

first (left) peak

1

bump on the right side of the first peak

1

second peak

1

The ranks are all 1 (and this estimation as a whole will be denoted by [1,1,1]) since there observed are no significant signs of interparticle effects.

We will explore briefly about this rank estimation problem below.

6.1. Learning Points#

  • component peak

  • ssd.plot_component(ratio_curve=True)

  • scds = decomposition.compute_scds()

  • rank = scd_to_rank(scd)

6.2. Human Observation#

As can be speculated from the examples shown so far, human observation plays a key role in the rank estimation. Roughly speaking, the rank of data is at least the number of visible peaks.

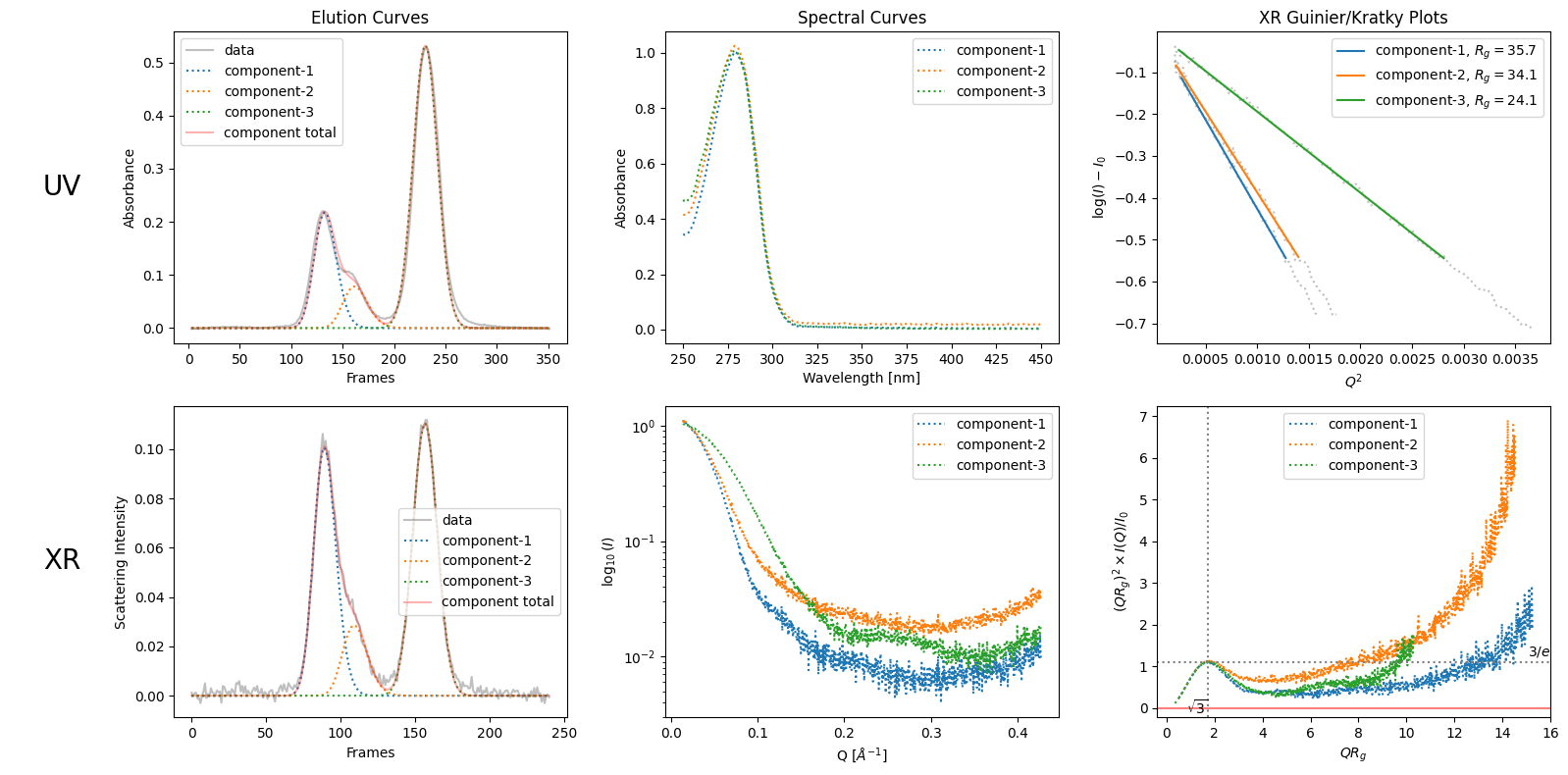
By observig the elution curves, humans can guess the number of components. For example as in the case of SAMPLE1 data, like decomposing into three seems better than two due to the bump in the right side of the first visible peak. See the difference in the following ddecompositons: the first one with two components (from default rough recongnition) and the second one with explictily specified three components.

from molass import get_version
assert get_version() >= '0.2.0', "This script requires molass version 0.2.0 or higher."
from molass_data import SAMPLE1
from molass.DataObjects import SecSaxsData as SSD
ssd = SSD(SAMPLE1)
trimmed_ssd = ssd.trimmed_copy()
corrected_ssd = trimmed_ssd.corrected_copy()
decomposition = corrected_ssd.quick_decomposition();
decomposition.plot_components();

zeros at the angular ends of error data have been replaced with the adjacent values.
../../_images/ebe2848ba092a9a5da143d2eab9fe56170efc039e82da989ed9b332b3b1f8fee.png 
decomposition_nc3 = corrected_ssd.quick_decomposition(num_components=3)
decomposition_nc3.plot_components();
../../_images/2d52e41912f625b93ace3b45e1ca49728c0c23fd09c1070f0b285e2f1850ae81.png

6.3. Absorbance / Scattering Ratio#

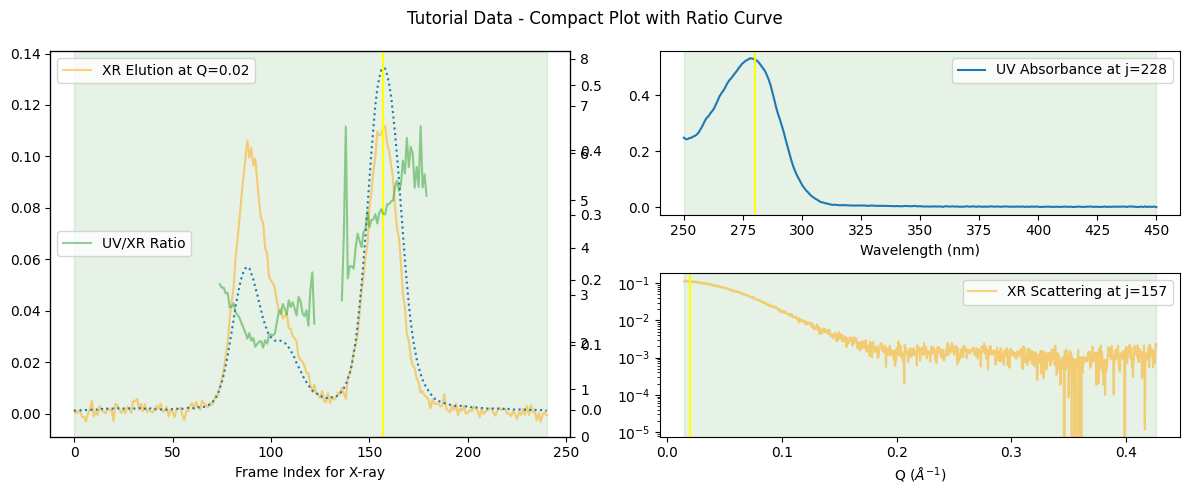
Sometimes, it can be useful if we observe the curve of the ratio variation between the absorbance and the scattering. We can plot it with the ratio_curve option as shown below.

corrected_ssd.plot_compact(ratio_curve=True, title="Tutorial Data - Compact Plot with Ratio Curve");
../../_images/aabbce0381679665841f962d8a785ea51226f9b43138ff07a6ec888e2a31f624.png

6.4. Concentration Dependence#

6.4.1. Relation between SCD and Rank#

Another method of rank estimastion is to compute the SCD - Score of Concentration Dependence - of each component peak. Using SCD’s, you can roughly distinguish the rank of a component peak according the the table below.

SCD value range

Rank distinction

less than 2

probably 1

between 2 and 5

uncertain

greater than 5

probably 2

We will give some examples of SCD computation below.

6.4.2. SAMPLE1 - Case of no concentration dependence#

scds = decomposition_nc3.compute_scds()
scds

[0.5141964291028607, 4.1353581642850905, 0.6386070838487024]

from molass.Backward.RankEstimator import scd_to_rank
ranks = [scd_to_rank(scd) for scd in scds]
for scd, rank in zip(scds, ranks):
    print(f"SCD: {scd}, Rank: {rank}")

SCD: 0.5141964291028607, Rank: 1
SCD: 4.1353581642850905, Rank: 1
SCD: 0.6386070838487024, Rank: 1

6.4.3. SAMPLE3 - Case of significant concentration dependence#

from molass_data import SAMPLE3
ssd3 = SSD(SAMPLE3)
decomposition3 = ssd3.quick_decomposition()
scds = decomposition3.compute_scds()
scds

[5.136732388051838]

ranks = [scd_to_rank(scd) for scd in scds]
for scd, rank in zip(scds, ranks):
    print(f"SCD: {scd}, Rank: {rank}")

SCD: 5.136732388051838, Rank: 2
Contents